무한 평판이 만드는 전기장 문제

 

이번에는 무한 평판(infinite plate)이 만들어내는 전기장(electric field)을 두 가지 방법을 이용해서 풀어볼 예정이다.

 

먼저 문제의 계산을 쉽게하기 위해서 문제 설정을 해보자. 무한 평판의 경우 $z = 0$에 있는 $xy$ 평면이라고 설정하자. 문제의 간결함을 위해서 평판의 두께는 무시하며 표면 전하 밀도(surface charge density)는 $\sigma$로 균일한 문제를 풀자.

 

그렇게 한다면 평판위의 한 점은 $(x, y, 0)$의 형태를 가지고 있다. 이제 이 평판에서 $z_0$만큼 떨어진 평판 외부의 한 점 $P$에서의 전기장을 찾아보자.

 

계산의 편의성을 위해서 $P$의 $x$ 좌표(coordinate)와 $y$ 좌표를 $0$으로 설정하자. 이렇게하면 이 점이 평판으로 사영(projection)된 점이 이 좌표계의 원점 $O$가 된다. 다시말해 $P$의 좌표는 다음과 같다.

$$P = \begin{pmatrix} 0 & 0 & z_0 \end{pmatrix} \tag{1}$$

 

$x$ 좌표와 $y$ 좌표를 다르게 잡아서 원점을 다른 곳에 놓은 문제를 풀 수도 있지만 이 경우 계산에 더 복잡한 상수항만 추가될 뿐 결과물이 기술하는 물리계는 똑같은 상황을 기술하게 된다.

 

이런식으로 전자기(electromagnetism) 문제에서는 좌표계 설정에 자유도(degree of freedom)이 존재한다. 자세한 내용은 다른 글에서 다루고 지금은 문제의 설정의 정당성만 확보하고 넘어가도록 하자.

 

 

이제 전기장의 공식을 이용해서 평판 위의 한 점 $Q$ 주변의 미소 면적(infinitesimal) $da$가 점 $P$에 만드는 전기장 $\vec{E}_Q$를 생각해보자. 먼저 $Q$의 좌표가 $(x, y, 0)$의 형태였으므로 이를 이용하면 다음과 같다.

$$\vec{E}_Q = \frac{\sigma}{4 \pi \epsilon_0} \frac{1}{x^2 + y^2 + z_0^2} da \hat{s} \tag{2}$$

이때 $\hat{s}$는 점 $Q$에서 점 $P$를 가르치는 단위 벡터(unit vector)를 의미하자.

 

이제 평면 위의 각각의 면적 요소들이 점 $P$에 만드는 전기장을 하나하나 더하면 된다. 그런데 평판위의 점들은 수학적 연속성(continuous)를 가진 대상이라고 가정한다면 적분(integral)을 통해서 덧셈을 할 수 있다.

 

즉, 식 (2)를 응용해서 다음과 같은 적분을 한다면 무한 평판의 각 점들의 전하(electric charge)가 점 $P$에 만드는 전기장을 모두 더한 전체 전기장(total electric field)이 된다.

$$\vec{E} = \frac{\sigma}{4 \pi \epsilon_0} \int \frac{1}{x^2 + y^2 + z_0^2} \hat{s} \; da \tag{3}$$

전하 밀도는 균일한 상수이기 때문에 적분 바깥으로 나올 수 있다.

 

먼저 $\hat{s}$를 구해보자. 점 $Q$의 위치 좌표를 $\vec{r}$, $P$의 위치 좌표를 $\vec{p}$라고 하면 두 점을 잇는 벡터 $\vec{s}$는 다음과 같다.

$$\vec{s} = \vec{p} - \vec{r} = -x \hat{x} - y \hat{y} + z_0 \hat{z} \tag{4}$$

 

이제 단위 벡터의 정의를 이용해서 $\hat{s}$를 구해보자.

$$\hat{s} = \frac{\vec{s}}{|\vec{s}|} = \frac{-x \hat{x} - y \hat{y} + z_0 \hat{z}}{\sqrt{x^2 + y^2 + z_0^2}} \tag{5}$$

 

지금까지 데카르트 좌표계(Cartesian coordinate)를 사용했기 때문에 면적 요소(area element) $da$는 다음과 같이 쓸 수 있다.

$$da = dx dy \tag{6}$$

 

이제 식 (5)의 결과와 식 (6)의 결과를 식 (3)에다 대입하자. 무한 평판의 경우 $xy$ 평면에 무한히 펼쳐져 있기 때문에 적분 범위는 무한대(infinity)로 주어진다.

$$\begin{split} \vec{E} = & \frac{\sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \frac{-x \hat{x} -y \hat{y} + z_0 \hat{z}}{\left( x^2 + y^2 + z_0^2 \right)^{\frac{3}{2}}} \; dx dy \\ = & \left[ \frac{\sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \frac{-x}{\left( x^2 + y^2 + z_0^2 \right)^{\frac{3}{2}}} \; dx dy \right] \hat{x} \\ & + \left[ \frac{\sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \frac{-y}{\left( x^2 + y^2 + z_0^2 \right)^{\frac{3}{2}}} \; dx dy \right] \hat{y} \\ & + \left[ \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty}  \frac{1}{\left( x^2 + y^2 + z_0^2 \right)^{\frac{3}{2}}} \; dx dy \right] \hat{z} \end{split} \tag{7}$$

 

식 (7)에서 유념히 봐야할 점이 전기장의 $x$ 성분과 $y$성분의 경우 홀함수(odd function)이라는 점이다. 홀함수의 성질에 따라 $(-\infty, \infty)$에서 적분을 하면 $0$이 된다. 굳이 귀찮은 적분을 일일히 하지 않아도 된다.

 

이제 전기장이 $z$ 성분만 가짐을 알 수 있다. 이는 무한 평판의 경우 한 점 $Q$가 만드는 전기장의 $x$ 성분과 $y$ 성분의 경우 이를 상쇄시키는 반대 위치의 점 $Q^{\prime}$이 반드시 존재하기 때문으로 이해할 수 있다.

 

 

이제 전기장의 $z$ 성분에 있는 적분을 마무리 해보자.

$$\vec{E} = \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \frac{1}{\left( x^2 + y^2 + z_0^2 \right)^{\frac{3}{2}}} \; dx dy \tag{8}$$

 

먼저 $x$의 적분을 하기 위해서 $y^2 + z_0^2 = a^2$, $x = a \tan{\theta}$로 치환(substitution)해보자. 이때 $dx$는 다음과 같이 주어진다.

$$dx = \frac{a}{\cos^2{\theta}} d \theta \tag{9}$$

 

탄젠트(tangent) 함수의 성질에 따라 적분 범위는 $\left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$로 바뀌므로 식 (8)은 다음과 같이 변형된다.

$$\vec{E} = \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\frac{pi}{2}}_{-\frac{\pi}{2}} \frac{1}{\left( a^2 (1 + \tan^2 \theta )\right)^{\frac{3}{2}}} \frac{a}{\cos^2 \theta} \; d \theta dy  \tag{10}$$

 

이제 $1 + \tan^2 \theta = \frac{1}{\cos^2 \theta}$라는 사실을 이용하면 다음과 같이 간단하게 변한다.

$$\vec{E} = \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \frac{1}{a^2} \cos \theta \; d \theta d y = \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\infty}_{-\infty} \frac{2}{y^2 + z_0^2} \; dy \tag{11}$$

 

이번에는 $y = z_0 \tan \phi$라고 치환하자. 그렇다면 식 (11) 또한 다음과 같은 적분으로 변하며 간단한 결과가 나온다.

$$\vec{E} = \frac{z_0 \sigma}{4 \pi \epsilon_0} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \frac{2}{z_0^2 (1 + \tan^2 \phi)} \frac{z_0}{\cos^2 \phi} \; d \phi \hat{z} = \frac{\sigma}{4 \pi \epsilon_0} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} 2 \; d \phi \hat{z} = \frac{\sigma}{2 \epsilon_0} \hat{z} \tag{12}$$

 

식 (12)에서 전기장이 아주 간결한 형태로 나타났음을 알 수 있다. 이 결과에 대한 분석을 진행하기에 앞서서 이번엔 가우스 법칙(Gauss' law)를 이용하여 문제를 풀어보자.

 

 

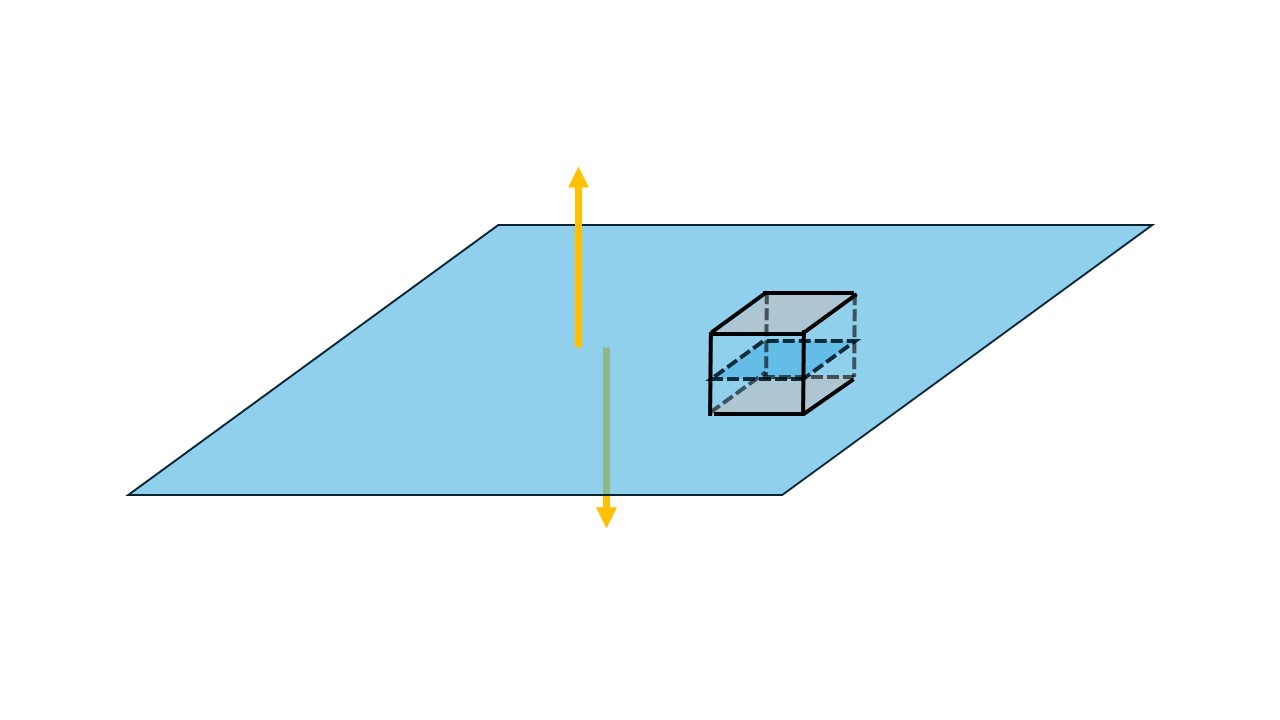
가우스 곡면(Gauss surface)의 경우 여러 방법이 있지만 가장 널리 알려진 방법은 밑면의 넓이가 $A$면서 동시에 $xy$ 평면이 밑면과 평행(parallel)하게 중앙을 가르지르는 직육면체(cuboid) 형태를 잡는 것이다.

 

우리는 평면에서 $z_0$만큼 떨어진 위치의 전기장을 알고 싶기 때문에 직육면체의 높이는 $2 z_0$가 됨을 알 수 있다.

 

가우스 곡면 내부의 전하량은 무한 평판의 전하량 밖에 없으므로 $Q = \sigma A$로 주어진다. 따라서 가우스 법칙은 다음과 같이 쓰인다.

$$\oint \vec{E} \cdot d \vec{a} = \frac{\sigma A}{\epsilon_0} \tag{13}$$

 

직육면체를 중심으로 데카르트 좌표를 잡고 직육면체의 밑변의 길이를 각각 $x_0$, $y_0$라고 잡으면 $A = x_0 y_0$이고 면적 벡터는 다음과 같은 6개의 경우가 존재한다.

$$\begin{split} \oint d \vec{a}_1 = & y_0 z_0 \hat{x} \\ \oint d \vec{a}_2 = & - y_0 z_0 \hat{x} \\ \oint d \vec{a}_3 = & x_0 z_0 \hat{y} \\  \oint d \vec{a}_4 = & - x_0 z_0 \hat{y} \\ \oint d \vec{a}_5 = & A \hat{z} \\ \oint d \vec{a}_6 = & -A \hat{z} \end{split} \tag{14}$$

 

이제 좌변의 적분을 생각해보자. 직육면체 표면에 수직 방향 전기장들을 더해야 하는데 아까 전 풀이 방식에서 보듯이 $x$ 성분과 $y$ 성분은 반드시 무한 평면 어딘가에 상쇄시켜주는 전기장을 만드는 점이 존재한다.

 

이를 문제의 대칭성(symmetry)으로 이해하기도 한다. 무한 평판 문제의 경우 점 $P$를 $xy$ 평면에 평행한 평면을 따라 회전하면서 바라봐보자. 무한 평면의 특성상 어디에서 바라보던 간에 항상 똑같은 상황이 펼쳐짐을 알 수 있다.

 

이를 회전 대칭성(rotational symmetry)이 있는 경우라고 말하는데 만약 전기장의 $x$ 성분과 $y$ 성분이 특정 방향으로 존재한다면 이 전기장은 어느 방향에서 바라보느냐에 따라서 전기장을 다르게 기술하게 된다.

 

이러한 모순(contradict)를 해결하기 위해서는 전기장의 $x$ 성분과 $y$ 성분은 회전 대칭성에 의해 $0$이 되어야 한다.

 

그럼 전기장이 지나가는 가우스 곡면은 무한 평판의 위에 있는 직육면체의 밑면과 아래 있는 밑면 밖에 없다. 또한 무한 평판이 직육면체의 중앙을 지나므로 윗면과 아랫면에서의 전기장은 서로 같으며 방향이 다르다.

$$\vec{E} (z = z_0) = E_z \hat{z} \tag{15}$$

$$\vec{E} (z = -z_0) = - E_z \hat{z} \tag{16}$$

 

식 (15)와 (16)의 결과와 식 (14)에서 $d \vec{a}_5$와 $d \vec{a}_6$의 벡터들을 각각 알맞게 내적시켜서 계산하면 식 (13)의 좌변은 다음과 같다.

$$\oint \vec{E} \cdot d \vec{a} = \oint E_z \; d \vec{a}_5 + \oint E_z \; d \vec{a}_6 = 2 E_z A \tag{15}$$

 

이를 식 (13)에 대입하면 다음과 같은 결과를 최종적으로 얻게 된다.

$$2 E_z A = \frac{\sigma A}{\epsilon_0} \tag{16}$$

$$\therefore \vec{E} = E_z \hat{z} = \frac{\sigma}{2 \epsilon_0} \hat{z} \tag{17}$$

 

식 (17)의 결과는 식 (12)의 결과와 일치함을 알 수 있다. 전기장의 정의를 이용해서 바로 구하는 방법도 있지만 가우스 법칙을 이용하면 비교적 손쉽게 전기장을 구할 수 있었다.

 

 

또한 이 식들의 놀라운 결과는 무한 평판 바깥에서의 전기장의 크기가 거리에 의존하지 않는다는 점이다.

 

일반적으로 사용되는 쿨롱 법칙(Coulomb's law)에서 기인한 전기장의 정의의 경우 전하에서 멀어질 수록 전기장의 세기가 약해진다.

 

하지만 식 (12)와 (17)의 결과를 통해 무한 평판의 경우 평판에서 얼마나 멀어지든 관계없이 전기장의 세기가 일정함을 알 수 있다. 이는 아주 간단한 원리를 통해서 정성적인 이해가 가능하다.

 

먼저 무한 평판의 전기장의 경우 $z$ 방향 성분을 제외한 나머지 성분은 전부 상쇄가 된다. 그런데 한 면적 요소가 만드는 전체 전기장 중에서 $z$ 방향 성분이 차지하는 비중은 점이 가까우면 가까울수록 커진다.

 

특히 점 $P$의 연직 아래에 있는 점 $O$가 만드는 전기장의 경우 해당 점이 만든 모든 전기장은 $z$ 성분에만 기여한다.

 

더욱이 멀어지면 멀어질 수록 전기장의 세기 자체도 약해지므로 점 $O$에서 멀어질수록 면적 요소가 기여하는 전기장의 세기는 급감함을 알 수 있다.

 

 

그래서 점 $O$를 중심으로 원(circle)의 형태를 그리는 적당한 범위를 생각해서 해당 범위 안의 전하들이 대부분의 전기장에 기여한다고 생각해보자.

 

이 범위를 규정할 때 원의 한 점에서 점 $P$까지의 직선을 그려서 이 직선과 $xy$ 평면이 이루는 각도(angle)을 기준으로 범위를 규정하도록 하자. 즉, 특정 각도까지가 유효한 범위가 되며 더 작은 각도는 그 기여도가 미미하다.

 

이제 점 $P$를 두 배 멀리하면 각 면적 요소들이 만들어내는 전기장은 $\frac{1}{4}$로 작아진다. 그렇지만 유효 범위를 그리는 원은 거리와 면적의 비례 관계를 통해 기존에 비해 $4$배가 커짐을 알 수 있다.

 

면적이 $4$배로 커진다는 의미는 전하량이 $4$배 많아진다는 의미이며 이는 거리가 멀어지면서 약해진 전기장을 많아진 전하가 보충하는 방식으로 작동한다. 따라서 전기장은 거리에 의존하지 않는 형태가 된다.

 

 

가우스 법칙의 유도

 

전기력과 전기장...장이란?