벡터, 정확히 알고 있나요? 벡터의 연산

이번 글에서는 자주 쓰는 벡터(vector)의 연산들을 정리해보도록 하겠다. 지난번 글과 마찬가지로 여기서 다루는 벡터들은 유클리드 벡터(Eucliead vector)이며 다른 일반화됐거나 특수한 연산에 대해서는 필요할 때 다루도록 하겠다.

 

 

1. 벡터의 덧셈과 뺄셈

먼저 벡터의 덧셈과 뺄셈을 구해보자. 사실 벡터를 정의하는 부분에서 벡터간의 덧셈은 결합 법칙(associativity)과 교환 법칙(commutativity)를 따르며 또한 덧셈에 대한 역원(inverse)가 존재해서 역원을 이용해 뺄셈을 정의했다.

 

이번엔 유클리드 벡터의 경우 어떻게 덧셈과 뺄셈을 계산하는지 보자. 먼저 임의의 \(n\)차원 벡터에 대해 다음과 같이 두 벡터를 직교 성분(orthogonal component)으로 나눠서 표현할 수 있다.

$$ \vec{A} = A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \tag{1} $$

$$ \vec{B} = B_1 \hat{e}_1 + B_2 \hat{e}_2 + B_3 \hat{e}_3 + \cdots + B_n \hat{e}_n \tag{2}$$

 

두 벡터들의 연산은 각 성분들의 연산으로 바꿔서 계산이 가능하다.

$$\begin{matrix} \vec{A} \pm \vec{B} & = & \left[ A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \right] \pm \left[ B_1 \hat{e}_1 + B_2 \hat{e}_2 + B_3 \hat{e}_3 + \cdots + B_n \hat{e}_n \right] \\ & = & (A_1 \pm B_1) \hat{e}_1 + (A_2 \pm B_2) \hat{e}_2 + (A_3 \pm B_3) \hat{e}_3 + \cdots + (A_n \pm B_n) \hat{e}_n \end{matrix} \tag{3}$$

 

 

이 연산 법칙을 조금만 바꾸면 다음과 같은 연산들도 생각할 수 있다.

$$\begin{matrix} \vec{A} + \vec{A} & = & \left[ A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \right] + \left[ A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \right] \\ & = & 2A_1 \hat{e}_1 + 2A_2 \hat{e}_2 + 2 A_3 \hat{e}_3 + \cdots + 2 A_n \hat{e}_n \\ & = & 2(A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n) \\ & = & 2 \vec{A}  \end{matrix} \tag{4}$$

$$\begin{matrix} \vec{A} - \vec{A} & = & \left[ A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \right] - \left[ A_1 \hat{e}_1 + A_2 \hat{e}_2 + A_3 \hat{e}_3 + \cdots + A_n \hat{e}_n \right] \\ & = & 0 \hat{e}_1 + 0 \hat{e}_2 + 0 \hat{e}_3 + \cdots + 0 \hat{e}_n \\ & = & \vec{0} \end{matrix} \tag{5}$$

 

지금보면 식 (5)에서 벡터의 정의에서 사용했던 덧셈의 항등원(identity)이 성분으로 어떻게 쓰는지 나타났다. \( \vec{0} \)으로 표현하기 보다는 간단하게 \( 0 \)으로 많이 쓴다. 나도 앞으로 그렇게 쓸 예정이다. 이 덧셈의 항등원을 영벡터(zero vector)라고 한다.

 

 

2. 내적(inner product)

이번엔 벡터 사이의 곱셈을 구해보려고 한다. 우리가 유용하게 쓰는 벡터 사이의 곱셈이 2개 있다. 결과가 스칼라(scalar)냐 벡터냐에 따라 두 곱셈의 연산을 구분한다. 먼저 볼 곱셈은 스칼라가 나오는 내적이다.

 

내적은 스칼라곱(sclar product) 또는 점곱(dot product) 등으로도 부르지만 이는 벡터에 스칼라를 곱하는 연산과 이름이 헷갈리기 때문에 나는 내적으로 통일할 것이다. 내적은 다음과 같은 계산을 의미한다.

$$ \vec{A} \cdot \vec{B} = (A_1 * B_1) + (A_2 * B_2) + (A_3 * B_3) + \cdots + (A_n * B_n) \tag{6}$$

 

벡터 \( \vec{A} \)에서 \(A_i \hat{e}_i \)와 같이 특정 방향과 성분을 생각할 수 있다. 이를 \( i \)방향으로의 \( \vec{A} \)의 사영(projection)이라고 부른다. 지금보면 내적은 각각 방향의 사영 성분끼리 곱해 더했음을 알 수 있다.

 

사실 식 (6)과 같은 계산은 지금 기저(basis)의 방향을 전부 수직하게 잡았기 때문에 발생한다. 만약 수직하지 않은 기저를 잡았을 경우 식 (6)과 같이 쓸 수는 없다. 하지만 많은 경우 수직한 기저를 잡기 때문에 유용한 공식이라고 할 수 있다.

 

 

심지어 내적을 이용하면 벡터의 크기도 구체적으로 계산할 수 있다. 지난 글에서 결과만 다루고 넘어갔었는데 내적을 이용해서 벡터의 크기, 노름(norm)는 다음과 같이 계산한다.

$$| \vec{A} |^2 = \vec{A} \cdot \vec{A} = A_1^2 + A_2^2 + A_3^2 + \cdots + A_n^2 \tag{7}$$
$$ \therefore |\vec{A}| = \sqrt{A_1^2 + A_2^2 + A_3^2 + \cdots + A_n^2} \tag{8}$$

 

특히 주목해야할 점은 식 (8)의 형태가 바로 \(n\)차원에서의 피타고라스의 정리(Pythagorean theorem)라는 사실이다. 유클리드 공간에선 식 (8)이 성립한다.

 

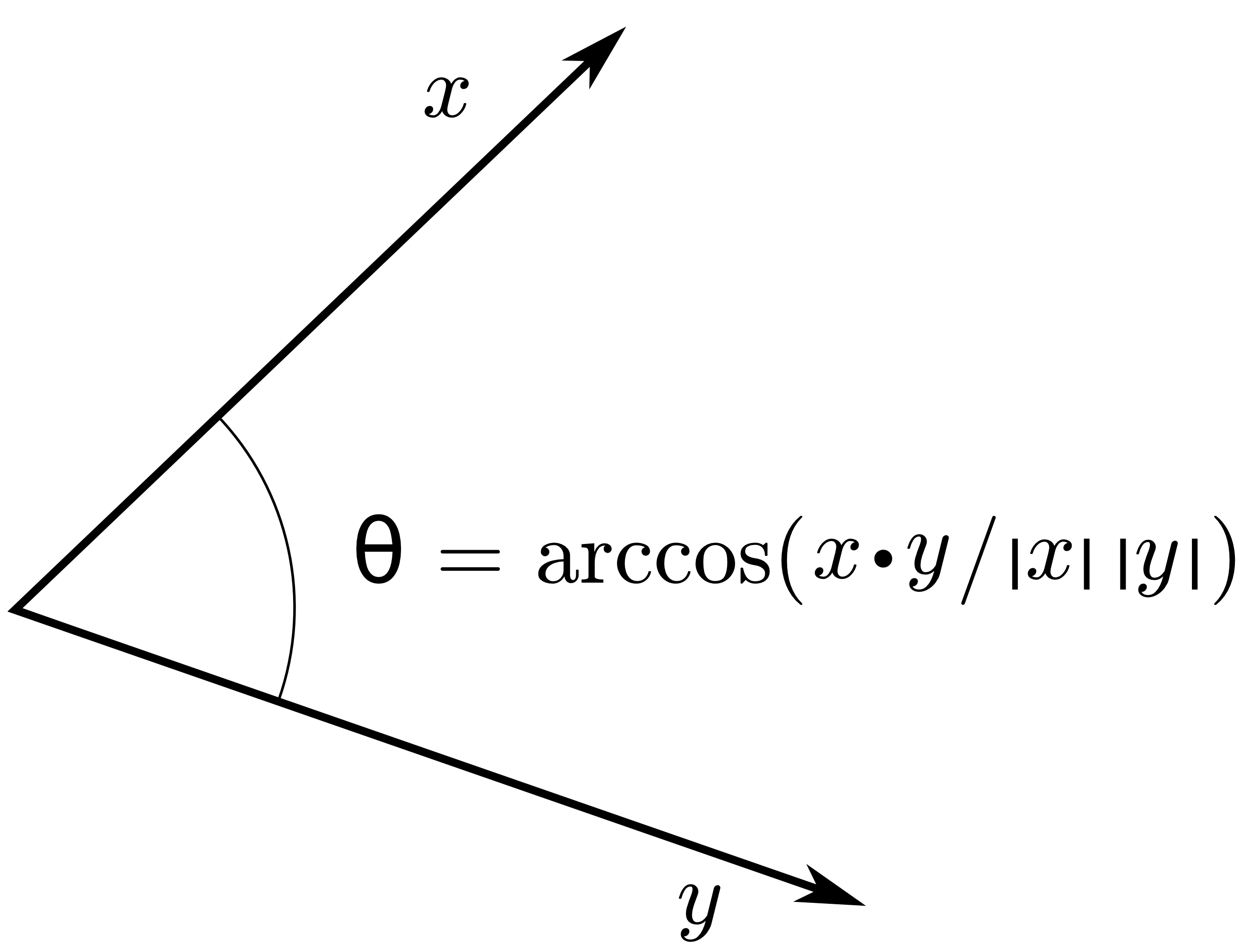
또한 유클리드 공간에서 내적에 대한 기하학적인 해석은 다음과 같은 식으로 나타난다. 여기서 각도 \( \theta \)는 두 벡터가 이루는 각도를 의미한다. 두 벡터가 만드는 각도 중 더 작은 각을 의미한다.

$$ \vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos{\theta} \tag{9}$$

 

식 (9)는 좌표로 표현한 벡터를 이용해서 두 벡터 사이의 각을 구할 때에도 사용된다.

$$ \theta = \arccos \left( \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|} \right) \tag{10}$$

 

 

식 (9)에 의거하면 서로 수직한 벡터의 내적은 \( 0 \)이 됨을 \( cos \)의 성질을 통해서 알 수 있다. 실제로 식 (6)의 방식을 써도 서로 같은 결과를 얻는다. 서로 수직인 벡터를 우리는 직교(orthogonal) 또는 수직(perpependicular)라고 부른다.

 

우리는 많은 경우 직교 기저를 잡으며 그래야 계산이 편리하다고 했다. 실제 문제에서 사용중인 기저가 서로 직교하는지 아닌지 확인하기 위해서 내적을 사용한다.

 

직교 기저의 경우 같은 방향 단위 벡터 사이의 내적은 \(1\)이되며 다른 방향 단위 벡터의 경우 수직하므로 내적이 \( 0 \)이 된다. 따라서 이를 일반화시키면 다음과 나타낼 수 있다.

$$ \hat{e}_i \cdot \hat{e}_j = \delta_{ij} \tag{11}$$

 

이때 식 (11)의 우항의 \( \delta_{ij} \)는 크로네커 델타(Kronecker delta)로 다음과 같은 성질을 가진다.

$$ \delta_{ij} = \begin{cases} 1 & \text{if} \; i = j \\ 0 & \text{if} \; i \neq j \end{cases} \tag{12}$$

 

 

벡터의 내적에는 다음과 같은 대수 관계들이 성립한다.

 

1 - 분배법칙(ditributive)

$$\vec{A} \cdot (\vec{B} + \vec{C}) = \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} \tag{13}$$

$$\begin{matrix} \vec{A} \cdot (\vec{B} + \vec{C}) & = & (A_1 \hat{e}_1 + A_2 \hat{e}_2 + \cdots + A_n \hat{e}_n) \cdot \left[ (B_1 + C_1) \hat{e}_1 + (B_2 + C_2) \hat{e}_2 + \cdots + (B_n + C_n) \hat{e}_n \right] \\ & = & A_1 (B_1 + C_1) + A_2 (B_2 + C_2) + \cdots + A_n (B_n + C_n) \\ & = & (A_1 B_1 + A_1 C_1) + (A_2 B_2 + A_2 C_2) + \cdots + (A_n B_n + A_n C_n) \\ & = & (A_1 B_1 + A_2 B_2 + \cdots + A_n B_n) + (A_1 C_1 + A_2 C_2 + \cdots + A_n C_n) \\ & = & \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} \end{matrix}$$

 

2 - 스칼라 곱에 대한 결합 법칙

$$\vec{A} \cdot (m \vec{B}) = (m \vec{A}) \cdot \vec{B} = m \vec{A} \cdot \vec{B} \tag{14}$$

$$\begin{matrix} \vec{A} \cdot (m \vec{B}) & = & (A_1 \hat{e}_1 + A_2 \hat{e}_2 + \cdots + A_n \hat{e}_n) \cdot (mB_1 \hat{e}_1 + mB_2 \hat{e}_2 + \cdots + mB_n \hat{e}_n) \\ & = & A_1(m B_1) + A_2 (m B_2) + \cdots + A_n (m B_n) \\ & = & (m A_1) B_1 + (m A_2) B_2 + \cdots + (m A_n) B_n \\ & = & (m \vec{A}) \cdot \vec{B} \\ & = & m A_1 B_1 + m A_2 B_2 + \cdots + m A_n B_n \\ & = & m \vec{A} \cdot \vec{B} \end{matrix}$$

 

3 - 교환법칙(commutative)

$$ \vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{A} \tag{15}$$

$$\begin{matrix} \vec{A} \cdot \vec{B} & = & A_1 B_1 + A_2 B_2 + \cdots + A_n B_n \\ & = & B_1 A_1 + B_2 A_2 + \cdots + B_n A_n \\ & = & \vec{B} \cdot \vec{A} \end{matrix}$$

 

 

3. 외적(outer product)

외적은 3차원 공간에서 성립하는 특수한 벡터의 곱셈이다. 물론 다차원으로 일반화 시킬 수 있는 방법도 있지만 대수학적인 개념이 많이 필요하므로 여기선 3차원에서 성립하는 특수 계산만 다루자.

 

외적은 가위곱(cross product)나 벡터곱(vector product)라고도 부르지만 이 중 벡터곱 같은 경우는 다른 계산과 이름에서 혼동이 오는 경우가 많으므로 나는 앞으로 외적으로만 부를 예정이다.

 

외적 계산은 \( \times \)로 표현하며 두 벡터의 외적은 다음과 같은 계산을 의미한다.

$$ \vec{A} \times \vec{B} = (A_y B_z - A_z B_y) \hat{x} + (A_z B_x - A_x B_z) \hat{y} + (A_x B_y - A_y B_x) \hat{z} \tag{16}$$

 

 

단위 벡터끼리의 외적은 다음과 같다.

$$\hat{x} \times \hat{y} = \hat{z} \tag{17}$$

$$\hat{y} \times \hat{z} = \hat{x} \tag{18}$$

$$\hat{z} \times \hat{x} = \hat{y} \tag{19}$$

 

두 벡터를 내적하면 두 벡터 모두에 수직인 새로운 벡터가 나옴을 알 수 있다. 두 벡터가 있으면 하나의 평면을 만들 수 있는데 이 평면에 수직한 벡터로 이해할 수 있다.

 

문제는 평면에 수직한 벡터는 2개라는 점이다. 우리는 오른손 법칙(right handed rule)을 이용해서 외적의 방향을 결정한다. \( \vec{A} \times \vec{B} = \vec{C}\)라는 문제의 경우 \( \vec{A} \)에서 \( \vec{B} \)로 오른손을 감을 경우 엄지 손가락의 방향이 \( \vec{C} \)의 방향이다.

 

 

그런데 오른손 법칙을 적용시키면 외적 순서에 따라서 다시 말해서 어떤 벡터부터 오른손을 감느냐에 따라서 결과 벡터의 방향이 바뀐다는 것을 알 수있다. 즉, 벡터는 내적과 달리 교환 법칙이 성립하지 않는다.

 

오른손 법칙을 이용해서 식 (17), (18), (19)의 순서를 바꿔보면 다음과 같이 된다.

$$\hat{y} \times \hat{x} = -\hat{z} \tag{20}$$

$$\hat{z} \times \hat{y} = -\hat{x} \tag{21}$$

$$\hat{x} \times \hat{z} = -\hat{y} \tag{22}$$

 

일반 벡터의 외적에 대해선 다음과 같은 반교환법칙(anti-commutation)이 성립한다.

$$\vec{A} \times \vec{B} = - \vec{B} \times \vec{A} \tag{22}$$

 

식 (16)의 계산 법칙과 외적의 반교환법칙은 행렬(matrix)를 안다면 좀 더 간단하게 일반화할 수 있다. 이는 다음에 행렬을 다루면서 일반화시켜보자.

 

 

외적의 기하학적인 계산은 다음과 같다.

$$ |\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin{\theta} \tag{23}$$

 

특히 이 법칙은 두 벡터가 만드는 평행사변형(rhombus)의 넓이랑 같다. \( |A| \sin{\theta} \)나 \( |B| \sin{\theta} \)가 평행사변형의 높이 역할을 해주기 때문에 알 수 있다. 심지어 식 (23)에 \( \frac{1}{2} \)를 곱하면 삼각형(triangle) 넓이 공식이 된다.

 

 

또한 벡터의 외적에는 다음과 같은 대수 관계가 성립한다.

 

1 - 분배 법칙

$$ \vec{A} \times (\vec{B} + \vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C} \tag{24}$$

$$\begin{matrix} \vec{A} \times (\vec{B} + \vec{C}) & = & (A_x \hat{x} + A_y \hat{y} + A_z \hat{z}) \times \left[ (B_x + C_x) \hat{x} + (B_y + C_y) \hat{y} + (B_z + C_z) \hat{z} \right] \\ & = & \left[ A_y (B_z + C_z) - A_z (B_y + C_y) \right] \hat{x} + \left[ A_z (B_x + C_x) - A_x (B_z + C_z) \right] \hat{y} \\ && + \left[ A_x (B_y + C_y) - A_y (B_x + C_x) \right] \hat{z} \\ & = & \left[ (A_y B_z - A_z B_y ) \hat{x} + (A_z B_x - A_x B_z) \hat{y} + (A_x B_y - A_y B_x) \hat{z} \right] \\ && + \left[ (A_y C_z - A_z C_y) \hat{x} + (A_z C_x - A_x C_z) \hat{y} + (A_x C_y - A_y C_x) \hat{z} \right] \\ & = & \vec{A} \times \vec{B} + \vec{A} \times \vec{C} \end{matrix}$$

 

2 - 스칼라 곱에 대한 교환 법칙

$$ ( m \vec{A} ) \times \vec{B} = \vec{A} \times (m \vec{B}) = m \vec{A} \times \vec{B} \tag{25}$$

$$\begin{matrix} (m \vec{A}) \times \vec{B} & = & ((mA_y) B_z - (m A_z) B_y) \hat{x} + ((mA_z) B_x - (mA_x) B_z) \hat{y} \\ && + ((m A_x) B_y - (mA_y) B_x) \hat{z} \\ & = & (A_y (m B_z) - A_z (m B_y)) \hat{x} + (A_z (m B_x) - A_x (m B_z)) \hat{y} \\ && + (A_x (mB_y) - A_y (mB_x)) \hat{z} \\ & = & \vec{A} \times (m \vec{B}) \\ & = & m( A_y B_z - A_z B_y) \hat{x} + m(A_z B_x - A_x B_z) \hat{y} + m(A_x B_y - A_y B_x) \hat{z} \\ & = & m \vec{A} \times \vec{B} \end{matrix}$$

 

 

또한 외적의 계산과 식 (9)를 이용하면 식 (23)을 유도할 수 있다. 다음과 같이 두 벡터의 외적의 크기를 구해보자.

$$(\vec{A} \times \vec{B}) \cdot (\vec{A} \times \vec{B}) = (A_y B_z - A_z B_y)^2 + (A_z B_x - A_x B_z)^2 + (A_x B_y - A_y B_x)^2 \tag{26}$$

 

이제 식 (26)의 우변을 전개해서 계산하면

$$\begin{matrix} (A_y B_z - A_z B_y)^2 + (A_z B_x - A_x B_z)^2 + (A_x B_y - A_y B_x)^2 \\ \\ = (A_y B_z)^2 - 2 A_y A_z B_z B_y + (A_z B_y)^2 + (A_z B_x)^2 - 2 A_z A_x B_x B_z + (A_x B_z)^2 \\ + (A_x B_y)^2 - 2 A_x A_y B_y B_x + (A_y B_x)^2 \\ \\ = A_x^2 (B_y^2 + B_z^2) + A_y^2 (B_x^2 + B_z^2) + A_z^2 (B_x^2 + B_y^2) \\ -2 A_y A_z B_z B_y -2 A_z A_x B_x B_z - 2 A_x A_y B_y B_x \\ \\ = A_x^2 (B_x^2 + B_y^2 + B_z^2) + A_y^2 (B_x^2 + B_y^2 + B_z^2) + A_z^2 (B_x^2 + B_y^2 + B_z^2) \\ - A_x^2 B_x^2 - A_y^2 B_y^2 - A_z^2 B_z^2 - 2A_y A_z B_z B_y - 2 A_z A_x B_x B_z -2 A_x A_y B_y B_x \\ \\ = (A_x^2 + A_y^2 + A_z^2) (B_x^2 + B_y^2 + B_z^2) - A_x B_x (A_x B_x + A_y B_y + A_z B_z) \\ -A_y B_y (A_x B_x + A_y B_y + A_z B_z) - A_z B_z (A_x B_x + A_y B_y + A_z B_z) \\ \\ = \vec{A}^2 \vec{B}^2 - (A_x B_x + A_y B_y + A_z B_z)^2 \\ \\ = |A|^2 |B|^2 - (\vec{A} \cdot \vec{B})^2 \\ \\ = |A|^2 |B|^2 - |A|^2 |B|^2 \cos^2{\theta} \end{matrix}$$

 

이제 마지막의 식을 삼각함수의 성질을 이용해서 바꾸면 된다.

$$(\vec{A} \times \vec{B})^2 = |\vec{A} \times \vec{B}|^2 = |A|^2 |B|^2 (1 - \cos^2{\theta}) = |A|^2 |B|^2 \sin^2{\theta} \tag{27}$$

$$\therefore \; |\vec{A} \times \vec{B}| = |\vec{A}||\vec{B}| \sin{\theta}$$

 

벡터, 정확히 알고 있나요? 수학적 정의

벡터, 정확히 알고 있나요? 벡터의 성질