리만 적분과 리만합

 

이번에는 구적법(quadrature)에서 사용했던 개념을 진화시켜 리만합(Riemann sum)과 리만 적분(Riemann integral)을 생각해보자.

 

지난 글에서는 원의 넓이를 구하는 방법으로 원을 잘게 쪼개서 재배열해서 더해 직사각형(rectangle) 모양을 만들어 직사각형의 넓이를 구하는 방식을 소개했었다.

 

이를 확장시켜서 어떤 둥근 곡선(curve)을 포함하는 도형의 넓이를 구할 때는 해당 도형을 잘게 쪼개서 쪼갠 넓이를 하나하나 구해서 더하는 방식으로 구한다.

 

 

이제 우리는 이러한 도형의 문제를 좌표 평면상에서 곡선 그래프와 $x$축 사이를 둘러싸고 있는 밑넓이를 구하는 문제로 바꿔서 다뤄보자. 이는 도형을 함수화시켜서 더욱 쉽게 다루고자하는 의도로 해석하면 좋다.

 

이제 넓이를 구하기 위해서 잘게 쪼개야 하는데 어떤 방식으로 잘게 쪼갤까? 하는 문제가 따라 붙는다. 이에 대해 리만 합으로 알려진 방법이 널리 알려져 있는데 이 방법을 소개해보겠다.

 

먼저 어떤 함수 $f(x)$를 구간(interval) $[a, b]$에서 $x$축과 둘러사는  밑넓이를 구하기 위해서 이 구간을 $n$등분해보자. 각각의 쪼갠 $x$들은 $a = x_0 < x_1 < \cdots < x_n = b$로 표현할 수 있다.

 

이렇게 어떤 구간을 더 작은 구간들로 쪼갤 경우 쪼갠 위치를 표현한 $x_i$들이 집합 $P$를 생각할 수 있다. 이러한 집합 $P$를 분할(partition)이라고 부른다.

$$P = \left\{ x_0, x_1, \cdots, x_n \right\} \tag{1}$$

 

이렇게 정의된 분할의 원소(element)들에는 그에 대응되는 함수값이 존재한다. 이 함수값을 높이로 삼고 잘게 쪼갠 구간의 길이 $\Delta x_i = x_i - x_{i-1}$를 밑변으로하는 직사각형들로 도형을 쪼갠다.

 

 

이때 어떻게 직사각형을 쪼개냐의 문제가 존재한다. 더 정확하게 표현하자면 "직사각형의 높이를 어떻게 설정해야 하는가?"라는 문제에 봉착하게 된다.

 

일단 우리가 구할 직사각형의 하나의 넓이를 개략적으로 생각해보면 다음과 같은 식을 따르게 된다.

$$A_i = f(x) \Delta x_i \tag{2}$$

 

문제는 식 (2) 함수 안의 $x$가 구간 $[x_{i-1}, x_i]$ 사이의 값 중 어떤 한 값을 설정할 수 있기 때문이다. 그리고 함수가 연속적으로 변하는 함수라면 어떤 $x$를 잡는가에 따라서 직사각형의 넓이가 조금씩 달라진다.

 

$x$를 잡는 방법에 대한 규칙을 줄 수 있는 몇 가지 방법을 생각해보자. 우선 어떤 $i$번째 구간에 대해 $x = x_{i-1}$로 잡아보자. 즉, 가장 왼쪽 함수값을 높이로 삼자. 그럼 넓이는 다음과 같다.

$$A^{left}_i = f(x_{i-1}) \Delta x_i \tag{3}$$

 

 

이제 이 식 (3)의 형태로 구한 직사각형의 넓이들을 다 더한 값을 $A^{left}$이라 하자. 이렇게 구한 리만합을 왼쪽 리만합(left Riemann sum)이라고 부른다.

$$A^{left} = \sum_{i=1}^n f(x_{i-1}) \Delta x_i \tag{4}$$

 

 

이와는 반대로 $x = x_{i}$로 잡아보자. 이렇게 만든 직사각형들의 넓이를 다 더한 값을 $A^{right}$라 하자. 이를 오른쪽 리만합(right Riemann sum)이라고 부른다.

$$A^{right} = \sum_{i=1}^n f(x_{i}) \Delta x_i \tag{5}$$

 

 

비슷하게 구간의 중앙 지점을 이용해보자. 정중앙은 $x = \frac{x_i - x_{i-1}}{2}$인 지점이다. 이를 중점 리만합(middle Riemann sum)이라고 부른다.

$$A^{middle} = \sum_{i=1}^n f \left( \frac{x_i - x_{i-1}}{2} \right) \Delta x_i \tag{6}$$

 

좀 특별한 경우로는 최대-최소 정리(extreme value theorem)를 응용해보자. 함수가 연속 함수일경우 임의의 닫힌 구간(closed interval)에는 반드시 최대값(local maximum)과 최솟값(local maximum)이 존재한다.

 

 

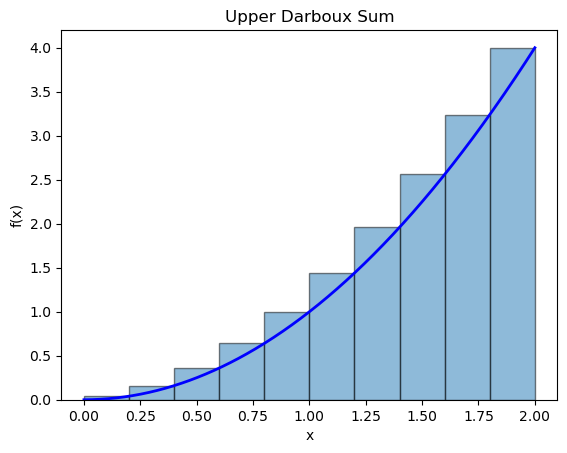
최댓값을 가지는 점을 $x_{max}$라하면 이 지점에서의 함수값인 최댓값을 높이로 삼아 직사각형의 높이를 구할 수 있다. 이 경우는 상합(upper Riemann sum) 또는 다르부 상합(upper Darboux sum)이라고 부르며 다음과 같이 넓이를 구한다.

$$A^{upper} = \sum_{i=1}^n f (x_{max}) \Delta x_i \tag{7}$$

 

 

마찬가지로 최솟값을 가지는 점을 $x_{min}$이라하면 이때 나오는 리만합을 하합(lower Riemann sum) 또는 다르부 하합(lower Darboux sum)이라고 부른다.

$$A^{down} = \sum_{i=1}^n f(x_{min}) \Delta x_i \tag{8}$$

 

 

여러가지 리만합이 존재하지만 결국 구간을 무한히 잘게 쪼개서, 즉 $n \rightarrow \infty$로가는 극한을 취할 경우 이 모든 리만합이 같은 값으로 수렴할 수 있다. 특히, 매끄러운 함수(smooth function)들은 모두 한 값으로 수렴한다. 이를 수식으로 표현하면 다음과 같다.

$$\lim_{n \rightarrow \infty} A^{left} = \lim_{n \rightarrow \infty} A^{right} = \lim_{n \rightarrow \infty} A^{middle} = \lim_{n \rightarrow \infty} A^{upper} = \lim_{n \rightarrow \infty} A^{down} = A \tag{9}$$

 

식 (9)와 같이 아주 잘게 쪼개는 극한을 취할 경우 모든 리만합이 같은 $A$로 수렴한다면 이를 리만 적분 가능(Riemann integrable)이라고 부른다. 또한 이런 방식의 적분법을 리만 적분이라고 부른다.

 

조건문으로 이루어진 아주 특수한 형태의 함수가 아니라면, 적어도 우리가 일반적으로 사용하는 대부분의 초월 함수(transcendental function)의 경우 리만 적분 가능 함수들로 모든 리만합이 하나의 값으로 수렴한다.

 

이렇게 얻어진 $A$는 해당 구간에서의 적분값과 같으며 이 넓이는 그래프와 $x$축이 이루는 면적의 넓이와 동일하다. 사실 구적법에서 착안한 아이디어에 해당한다.

$$\int_{a}^{b} f(x) \; dx = \lim_{n \rightarrow \infty} f(x) \Delta x \tag{10}$$

 

실제로 이 값이 적분과 일치함은 적분과 리만합의 극한이 어떤 임의의 양수 $\epsilon$보다 작음을 통해서 증명이 가능하지만 이번 글에서 다루기엔 너무 긴 내용이 되어 여기까지만 글을 작성하도록 하겠다.

 

 

원의 넓이와 구적법